The Number Sense Lens

Lenses are conceptual frameworks to organize ideas, skills, concepts, and developmental milestones. They provide educators with shared perspectives on expectations and outcomes, and provide ways to define and understand student learning to guide planning and instructional decision making. Lenses help to clarify, and focus attention.

Educators use a wide variety of lenses to understand and communicate about student learning.  In mathematics, the content and performance standards provide two helpful lenses, but there have been many lenses over time (e.g. NCTM’s Priciples and Standards, Battista’s CBA system, Math Recovery and AVMR, etc). There are differnt lenses for the many aspects of learning and development. Sometimes we look through social-emotional lenses with facets like, “Does the student have a group of friends they play with?” or, “Do they control their temper?” Lenses for understanding learning are often defined by the assessments we utilize to understand students. In reading, for example, we might talk about facets of literacy like phoneme blending, segmentation, or the ability to retell a story. Lenses are multi-faceted frameworks for how we see and talk about students.

Understanding and Assessing Number Sense

Mathematical thinking is best thought of as an interactive network of ideas. Concepts connect, and skills build upon one another within and across topics. Number sense is a subset of that interactive network. It is comprised of those facets of learning that make sense-making and reasoning possible, contributing to general development of mathematical thinking.

When we look at learning through the lens of number sense that means different things to different people. Number sense is complex and multifaceted and not easily defined. The Universal Screeners for Number Sense provide a framework for understanding number sense. The Number Sense Lens provides an organizational structure to help teachers understand and communicate about student learning.

Number sense is best understood as a collection of skills, concepts, and developmental stages. The Universal Screeners for Number Sense (USNS) assessments provide a way to assess the development of number sense. If you do not already have a copy of these open-source assessments, download your free copy today here. Using the USNS, facets of number sense are assessed repeatedly, within and across grade levels, growing in difficulty and complexity to match the expectations of the grade levels. The facets of number sense combine to help us understand each student’s growth and development, his/her strengths, and areas for improvement.

The Number Sense Lens

The Number Sense Lens developed for the USNS seeks to be specific and detailed enough to help teachers understand student development, which helps support targeted instructional responses.

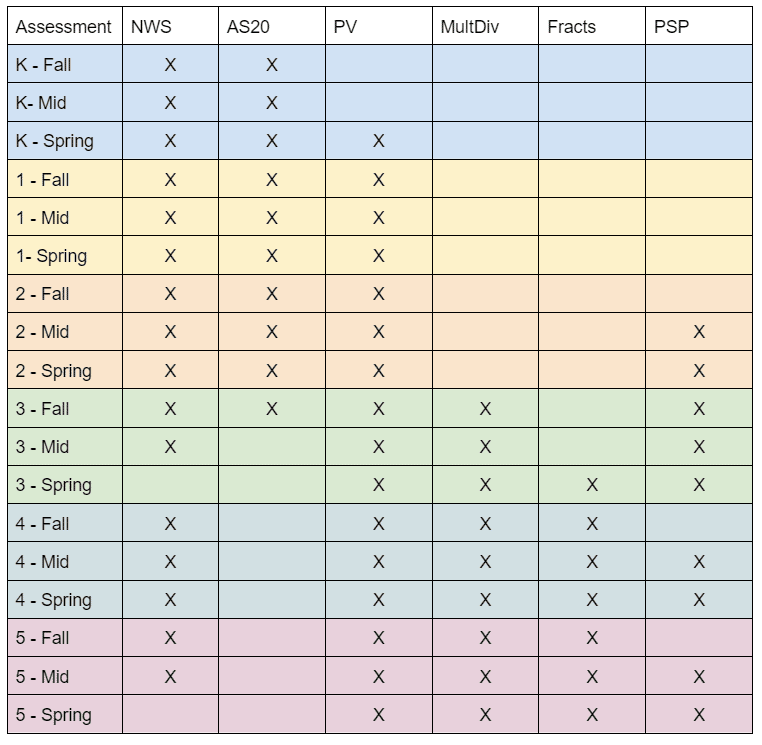
The 6 primary facets of the Number Sense Lens for Kindergarten – Grade 5:

• Numerals, Words, and Sequences (NWS)
• Addition and Subtraction within 20 (AS20)
• Place Value (PV)
• Multiplication & Division (MultDiv)
• Fractions (Fracts)
• Problem Solving and Problem Posing (PSP)

While the facets of the Number Sense Lens are defined and assessed in isolation, none stands alone; each is only a facet of the full lens. Learning progress across the facets is typically uneven, and unique for each student. Some students show strong conceptual understanding of addition and subtraction within 20, while they are still learning to accurately read and write numerals in that same range. Other students will show a strong command of verbal number sequences, while still learning to apply that knowledge to solve contextualized problems. The Number Sense Lens is designed to provide teachers with the insights and knowledge they need in order to better serve students and support their number sense development.

The Organization of the Number Sense Lens

The Number Sense Lens is organized into primary, secondary, and tertiary facets. For example, Numerals, Words and Sequences (NWS), the first primary facet is broken into Reading and Writing Numerals (RWN), and Sequences (Seq). In turn, these are also broken down into smaller components. For example, Reading and Writing Numerals (RWN) has two components – Numeral ID, and Writing Numerals.

For example, the organizational structure of Numerals, Words and Sequences can be seen like this:

• Numerals, Words and Sequences
  • Reading and Writing Numerals
    • Numeral ID
    • Writing numerals
  • Sequences
    • Forward Number Word Sequences
    • Backward Number Word Sequences
    • Number Lines
    • Skip Counting

This nested structure is used for the entire Number Sense Lens.

6 Facets of the Number Sense Lens

Facet 1: Numerals, Words and Sequences

The Numerals, Words, and Sequences facet of number sense includes foundational skills necessary for engaging and for supporting further learning. This facet includes the ability to read and write numerals, starting at the early grades with single digit numerals to large numbers, fractions, and decimal numbers at the upper grades. The reading and writing of numerals is directly connected to the words involved. Much of this is linguistic in nature, that is, a student might learn to read a number before clearly understanding the magnitude or place value structure of that number. Words also relate to the ability to recite verbal number sequences. These sequences are what we think of as verbal counting, forward, backward and skip counting. Sequences also relate back to their order in space, on the mental number line. Thus, the Numerals, Words and Sequences facet also includes understanding sequences and how they relate to number lines.

Facet 2: Addition and Subtraction Within 20

Addition and Subtraction Within 20 is assessed in grades K-3, and includes some of the most fundamental skills of early arithmetic and concept of number. The ideas of Addition and Subtraction Within 20 assessed using the USNS are separated into four components, the first of which is Counting and Cardinality. Counting and cardinality includes 1:1 correspondence, cardinality, fingers, and subitizing. The skills and concepts of counting and cardinality represent some of the most important aspects of early numerosity, and thus are focused on in detail early in the USNS assessment series.

Early addition and subtraction deals with the conceptualization of addition subtraction and the development of strategies for solving basic problems like 4 + 3. In order to elicit the reasoning of the student, this task is presented as a covered task. That is, 4 objects are presented to the student and then covered. Then 3 more objects are presented, and those too are covered. “How many are there in all?” For a young student, this is a complex problem, and there are subtleties that a trained eye will recognize as young students apply their number sense to solve this task. Thus, Covered Tasks represent one of the facets of Addition and Subtraction Within 20, because they help teachers to learn about students’ abilities to make sense of and reason about addition and subtractions in simple contexts.

Another facet of Addition and Subtraction Within 20 is defined as Structures, Flexibility and Fluency. This is the aspect of number sense that we observe when students have had so many experiences with combining and separating within 20 that they begin to know those combinations without the need for counting by ones. Structures – the ability to use landmark numbers like 5, 10 and doubling is one aspect of this idea. Flexibility is that ability to think of combinations in different ways – 5 and 5 makes ten, and so does 6 and 4. Fluency suggests that recalling the sums, differences, and part-part-whole relationships within 20, over time, with meaningful practice, becomes somewhat effortless. These aspects of number sense combine to represent an important milestone that students to apply to learn increasingly complex ideas.

The final aspect of the Addition and Subtraction Within 20 is Reasoning with Objects and Drawings. The ability to explain addition and subtraction using visual representations is assessed repeatedly on the kindergarten through 2nd grade screeners. This facet combines verbal and conceptual development. The ability to communicate reasoning and understand the reasoning of others is a practice that supports engagement and establishes the expectation that mathematics makes sense.

Facet 3: Place Value

Understanding and applying the ideas of place value is critical. However, place value is not as simple as asking a student, “Which digit is in the tens place?” Early learning of place value builds from the ability to conceptualize and operate with ones and tens. Take these examples:

Task 1:

The teacher presents a set of 10 dots in the form of a ten-frame, a widely used representation familiar to most students. “Here are ten dots.” Next the teacher presents a small array of 6 dots. “I am putting these six dots with the ten. How many dots are under here now?” This part of the task helps teachers to understand if the student knows basic ten-plus combinations; a critical first step in the understanding of place value. Some students will resort to counting all of the dots, starting from 1, not utilizing the ten despite the familiar structure. Others will use the ten and count on, “10, 11, 12, 13, 14, 15, 16.” This represents an important phase in the development of place value. Still other students will provide a quick, automatic response of 16, an ability which eventually all students will master, and a critical step toward solving problems like 30 + 6, 300 + 60, 16 – 6, etc.

Task 2:

Once the student has provided an answer for the first task, the teacher either confirms or demonstrates for the child that there are 16. The 16 dots are covered and another ten-frame is presented. “There are sixteen dots under here, and now I am adding another ten. How many dots are there now?” Students who have developed the ability to operate with tens and ones will quickly answer 26. You will hear students say things like. “Ten, …twenty, …and six, that’s twenty-six.” This shows that they can isolate the tens from the ones in order to solve the task. Other students might resort to counting on by ones, even those who initially answered 16 promptly without the need to count. This task reveals the students’ abilities to apply the structure of ones and tens to solve problems and helps teachers to understand which students are ready to handle more abstract and complex problems, and which students would benefit from scaffolds and supports as they approach addition and subtraction problems within and beyond 100.

The tasks above are grouped into the ideas of Ones, Tens, and Hundreds, a facet of Place Value. Another facet of Place Value is Magnitude and Comparison. The ability to use understandings of place value to compare and know the relative size of numbers is often considered a cornerstone of number sense. Magnitude and Comparison is assessed using traditional comparison problems and through the use of number lines and drawings.

The next aspect of Place Value in the Number Sense Lens is named Computation, Equations, and Procedures. Although the ability to utilize some of these, what might be considered rote aspects of mathematics is, in and of itself, not an indicator of number sense, the ability to compute – including using mental math, to use equations, and understand procedures – is an important piece of the larger picture.

Finally, Decimal Place Value has been added. Decimal place value, which is an important continuation of the work with whole numbers from the primary grades, is considered separately from those ideas because it represents an important next step in the learning; however, when considering students’ overall number sense development, it is important to consider decimal place value within the context of the students’ development of the ideas of Place Value as it relates to whole numbers.

Facet 4: Multiplication and Division

Multiplication and Division begins to be assessed in third grade on the USNS. This is not to say that these ideas only begin in third grade. When students form, count, and see equal groups in the earlier grades, this is important foundational work that will support sense making for years to come.

Multiplication and Division is separated into two parts: Computation, and Modeling and Representing. Computation includes a variety of skills and concepts. As students display their ability to utilize the structure of repeated groups to find products, factor, and solve problems related to division, this represents a series of important milestones in their number sense development.

Equally important is the ability to represent multiplication and division using visual models and drawings. This serves to help them express their reasoning and to understand the reasoning of others. Connected, and perhaps equally important is the ability to create equations and numeric representations of multiplicative relationships in the world around us. Seeing 6 sets of 3 as 3 + 3 + 3 + 3 + 3 + 3 is important. Knowing that this can also be represented as 6 x 3 becomes critical as number sense, and operational sense, become increasingly important in the intermediate grades.

Facet 5: Fraction Concepts

Making sense of fractions is critical. The USNS begins assessing fractional concepts in 3rd grade as do most standards and curricula across the United States. Fractional concepts are seen through three facets on the USNS. There are ideas related to Magnitude, Comparison, and Equivalence. Listening to how students mentally compare fractions can reveal much of how they understand fractions, how they understand the numerators and denominators, how they utilize benchmark fractions, and how they perceive two fractions as equivalent.

The second facet of Fraction Concepts in the Number Sense Lens is Representations. The idea of Representations includes the ability to interpret and create visual representations of fractions, area models, region models (including tape diagrams, circles, etc.), and number lines. Please note that fractional number lines are considered separately from whole number and decimal number lines that are included in Numerals, Words, and Sequences.

The final facet of Fraction Concepts is Computation. This facet includes concepts of addition, subtraction, multiplication and division ideas. This lens explicitly excludes procedural knowledge related to these ideas. Problems in the USNS are limited to contextualized problems (word problems) and mental math.

Facet 6: Problem Solving and Posing

Problem Solving and Posing is included as a separate facet, although connections to the other facets of the Number Sense Lens are frequent and recurring. It addresses the ability to apply what one knows about number and operations to solve problems in contexts and to create contexts for given equations. Those who are familiar with the Standards for Mathematical Practice will see connections with, “SMP #1: Make sense of problems and persevere in solving them,” and, “SMP #2: Reason abstractly and quantitatively.”

This facet of the Number Sense Lens also includes ideas related to what some call “operational sense.” That is, the connections that students make between formal, symbolic, abstract mathematics, and real world contexts. The ability to apply multiplication, when addition might also solve the problem, is an important milestone in a student’s mathematical development, and is important for educators to notice.

Problem Solving and Posing has two major parts: Solving and Posing. Solving includes all one and two step problems involving addition & subtraction and multiplication & division of whole numbers, decimals, and fractions. Special attention is given to measurement comparison problems. A series of questions in the USNS assess student’s ability to compare lengths. These problems reveal the capacity that a student has to coordinate two units (not being combined or separated) and to recognize that the value of the difference, “How much longer?” is visible in the empty space between the two. This series of questions runs across multiple grades starting with smaller numbers and ending with fractions in 5th grade.

Problem Posing, the ability to write a story problem to match a given equation, is the final component of the K-5 Number Sense Lens. This is assessed for addition, subtraction, multiplication, and division.

Special note:  At this time the Number Sense Lens only spans K-5. Interested in thinking about what the 6-8 Number Sense Lens should include? So are we. Contact us at screeners@forefront.education to get involved in the conversation.

Number Sense Lens and Forefront

The following section is for districts that have adopted Forefront®. Forefront allows schools and districts to collect and organize assessment results, such as USNS results, to inform and improve instruction, collaborative work, and grading and reporting out. If you are interested in learning more about Forefront, you may explore a self-guided demo account here or request a live demo.

For Forefront clients, the Number Sense Lens is a way to organize the aspects of number sense assessed using the USNS. Each of the questions has been associated with the framework, providing a multi-faceted lens through which to understand each student’s number sense development. If your school or district has a Forefront account, and you wish to have this Lens added to your courses, explore this support article or reach out to support.

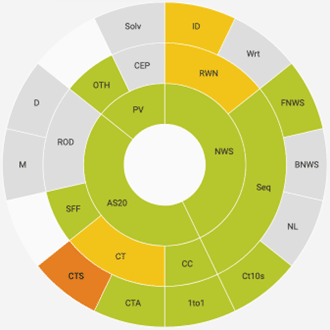
Here is an example of a kindergarten student’s wheel using the Number Sense Lens:

In the interface, the user can hover and click on each circle node to see the definitions of each of the facets of the Lens. What we see here is a wheel that is mostly green, indicating that the student is performing as is expected and likely no additional support will be necessary for the student. In this visual, a district is using orange and yellow colors to indicate areas where a student may need support with additional instruction and/or practice. These may also be areas that a teacher monitors or assesses further to gather additional evidence of learning.  Forefront enables teachers to quickly and easily understand the strengths of their students, their readiness for grade level content, and where additional attention should be given.  The Number Sense Lens in Forefront is an innovation to improve efficiencies, and to improve collaboration and communication.

In this case, the orange on the lower left represents a Covered Task involving subtraction, abbreviated as “CTS”. The yellow in the upper right is Numeral Identification (ID). Notice as well, the strengths in so many areas, including importantly Place Value: Ones, Tens, and Hundreds (OTH).

It should always be mentioned that the data collected via the levels of performance on the assessment only paints a piece of the picture, and that the notes, observations, and interpretations of the assessor complete the lens. Our team explores what it looks like to, Gather Quality Feedback from USNS Interviews, in this 40-minute presentation that focuses on more than collecting data points. Watch the webinar on-demand here.

Conclusion

Number sense is a fundamental and critical part of early mathematical thinking. There are many ways to reason and strategically solve mathematical problems, and that is the beauty and creativity in mathematics. All problems can be solved in different ways, and we should embrace that as educators. We hope you will find this Number Sense Lens a valuable conceptual framework to apply to your work to understand students’ number sense and support their development as mathematical thinkers.

View an on-demand presentation of the Number Sense Lens framework with David Woodward, the lead author of the USNS Project, here.

About the Author:

David Woodward is an educator with more than 25 years of experience as a classroom teacher and district leader in math education. He founded Forefront Education to help educators better understand student learning with meaningful assessments and support standards-based grading that is automatic, accurate, and reliable. David recently retired as a math coach at Boulder Valley School District in Colorado in June 2020. He leads the Universal Screeners for Number Sense project (formerly known as the BVSD K-5 Math Screeners). Read more.